Optimizing Risk and Cost in Supply-Demand Management by Simulating Probabilistic Outcomes

We developed a stochastic mixed-integer linear programming (MILP) framework that balances cost optimization with risk mitigation in supply chain scheduling by simulating probabilistic disruption scenarios. This principled approach improves supply chain resiliency over traditional deterministic cost-minimization by explicitly modeling block outages and idiosyncratic delays, while implicitly favoring supplier diversity. Ultimately, the risk-adjusted methodology leads to ~20% improvement in simulated safety stock compliance rate.

‍

The Real Cost of Supply Chain Disruptions

In 2024, a prolonged supplier outage put our manufacturing client within a week of a full production shutdown when 60% of their critical input deliveries were concentrated with one vendor. Their delivery schedule had balanced mitigating single-supplier risk while reducing transportation costs, but their risk thresholds were insufficient for the year’s challenge, creating a single point of failure.

This scenario repeats across industries: schedules that look perfect on paper but fail (sometimes, catastrophically!) in practice. Supply chain managers face an impossible choice—minimize costs through concentration or pay premiums for diversification without quantifying the risk reduction benefit.

We solved this by treating supply chain scheduling as a stochastic optimization problem, explicitly modeling uncertainty and optimizing for expected profit under realistic disruption scenarios rather than just minimizing deterministic costs.

The Recipe

1. We modeled empirical supplier delay distributions using skewed exponential distributions that fit historical data
2. We generated realistic disruption scenarios using Monte Carlo simulation of both systematic supplier failures and individual delivery delays
3. We created a stochastic mixed-integer linear program (MILP) with a risk-weighting parameter (λ) that optimizes across the scenarios, balancing deterministic cost minimization with risk mitigation

‍

Beyond Deterministic Cost Minimization

The Fundamental Problem

Traditional supply chain optimization solves:

minimize Σ(cost_ij * delivery_ij)
subject to:
    Σ(delivery_ij) >= safety_stock_i  ∀i  # Meet safety_stock
    Σ(delivery_ij) <= capacity_j  ∀j  # Respect capacity

This approach ignores two critical realities:

1. Supplier concentration risk - over-relying on single suppliers
2. Stochastic disruptions - real-world delays and outages

‍

Our Stochastic Formulation

We reformulate the problem as expected profit maximization under uncertainty:

class StochasticSupplyChainOptimizer:
    def __init__(self, scenarios, risk_weight=0.3):
        self.scenarios = scenarios # Sampled disruption scenarios
        self.λ = risk_weight # Cost vs risk trade-off parameter

    def optimize(self, safety_stock, suppliers, costs, constraints, revenue_per_unit):
        """Optimize expected profit across probabilistic scenarios"""

        # Decision variables
        x = cp.Variable((len(safety_stock), len(suppliers)), boolean=True)

        # Expected cost across scenarios
        expected_cost = 0
        expected_revenue_loss = 0

        for scenario in self.scenarios:
            # Apply delays/outages to this scenario
            delayed_deliveries = self.apply_disruptions(x, scenario)

            # Calculate revenue loss from unmet safety_stock
            unmet_safety_stock = cp.maximum(0, safety_stock - delayed_deliveries)
            scenario_revenue_loss = cp.sum(unmet_safety_stock * revenue_per_unit)

            expected_cost += scenario.probability * cp.sum(costs * x)
            expected_revenue_loss += scenario.probability * scenario_revenue_loss

        # Objective: minimize cost + revenue loss
        objective = (self.λ * expected_cost +
                    (1 - self.λ) * expected_revenue_loss)

        return cp.Problem(cp.Minimize(objective), constraints)

‍

Modeling Real-World Supply Chain Disruptions

Our disruption model captures two primary failure modes observed in production data:

1. Block Outages (Systematic Supplier Failures)

Major supplier disruptions that affect all deliveries from that supplier:

@dataclass
class BlockOutage:
    supplier_id: int
    start_week: int
    duration_weeks: int
    probability: float = 0.15  # e.g., 15% annual probability per supplier

def generate_block_outages(suppliers, time_horizon):
    """Generate block outage scenarios using empirical data"""

    outages = []
    for supplier in suppliers:
        # Bernoulli process for outage occurrence
        if np.random.random() < supplier.annual_outage_probability:
            start_week = np.random.randint(0, time_horizon)
            duration = np.random.randint(4, 13)  # e.g., 4-12 weeks historical range

            outages.append(BlockOutage(
                supplier_id=supplier.id,
                start_week=start_week,
                duration_weeks=duration,
                probability=supplier.annual_outage_probability
            ))

    return outages

‍

2. Idiosyncratic Delays (Individual Delivery Variability)

Random delays affecting individual deliveries, modeled with exponential tails:

def generate_idiosyncratic_delays(planned_deliveries):
    """Model supplier-specific shipment delays with heavy-tailed distribution"""

    delays = []
    for delivery in planned_deliveries:
        supplier = delivery.supplier
        
        if np.random.random() < supplier.delay_probability:
            delay_days = np.random.exponential(scale=supplier.average_delay)
            delays.append(delay_days)
        else:
            delays.append(0)

    return delays

‍

Scenario Generation and Monte Carlo Simulation

After fitting delay distributions to historical data, we generated supply chain scenarios that capture a range of possible disruptions. Our approach uses Monte Carlo simulation to create a representative sample of potential events rather than attempting to optimize against all possible futures.

Simulation Framework

class SupplyChainSimulator:
    def __init__(self, num_scenarios=1000):
        self.num_scenarios = num_scenarios

    def generate_scenarios(self, planned_schedule, suppliers):
        """Generate realistic disruption scenarios"""

        scenarios = []
        for _ in range(self.num_scenarios):
            scenario = Scenario(probability=1.0 / self.num_scenarios)

            # Generate block outages
            block_outages = self.generate_block_outages(suppliers)

            # Generate idiosyncratic delays
            individual_delays = self.generate_individual_delays(planned_schedule)

            # Apply disruptions to planned schedule
            disrupted_schedule = self.apply_disruptions(
                planned_schedule, block_outages, individual_delays
            )

            scenario.disrupted_deliveries = disrupted_schedule
            scenario.unmet_safety_stock = self.calculate_unmet_safety_stock(
                disrupted_schedule, safety_stock
            )

            scenarios.append(scenario)

        return scenarios

    def evaluate_schedule_robustness(self, schedule, scenarios):
        """Evaluate schedule performance across scenarios"""

        for scenario in scenarios:
            disrupted = self.apply_disruptions(schedule, scenario)

						# update metrics
            metrics['expected_cost'] = ...
            metrics['stockout_probability'] = ...
            metrics['expected_revenue_loss'] = ...            )

        return metrics

‍

Case Study: A risk-adjusted plan vs. a cost-minimal schedule

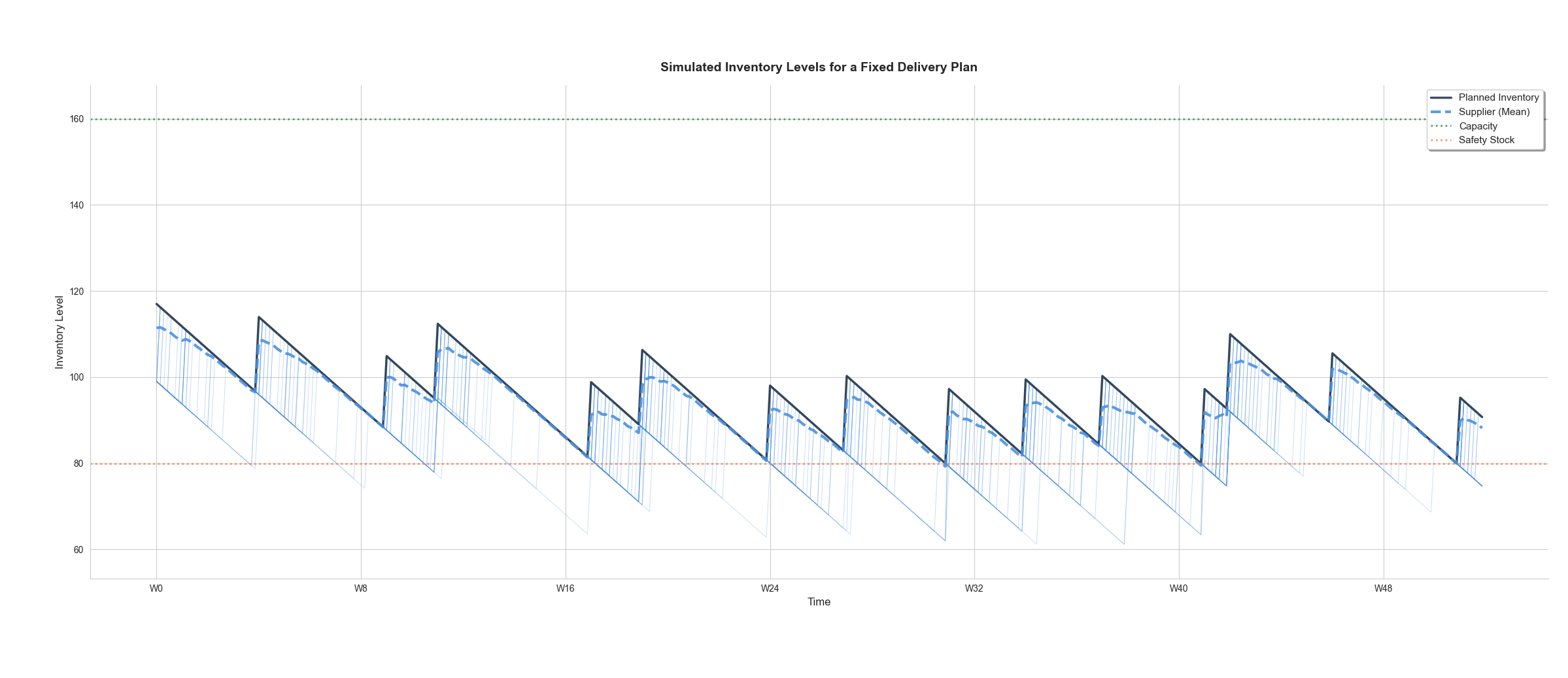
A key advantage of this framework is its visualization capabilities, showing how different scenarios affect delivery plans. In the example below, we display a fixed delivery plan for a single item's inventory level in charcoal. Several simulated scenarios appear in light blue, with the thick blue line representing the mean inventory level across all simulations.

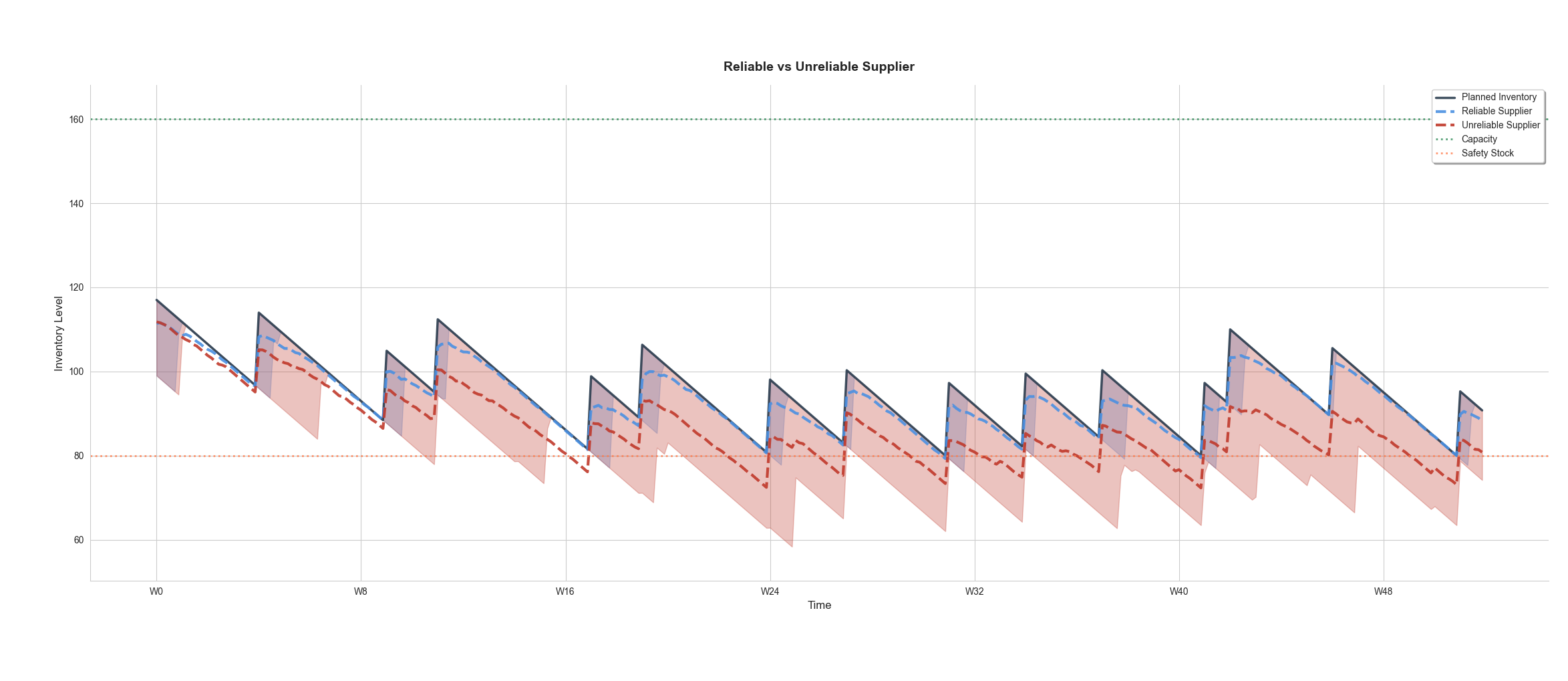
This framework provides an immediate visual assessment of how supplier reliability affects forecasted inventory levels. Below, we compare an unreliable supplier (red) experiencing more delays with a more reliable one (blue). Using a fixed delivery plan (charcoal), we simulate outcomes for both suppliers.

The shaded regions show the 20th to 80th percentile range of outcomes across all simulations for each supplier. It's clear that many scenarios involving the unreliable supplier fall below our preferred safety stock level.

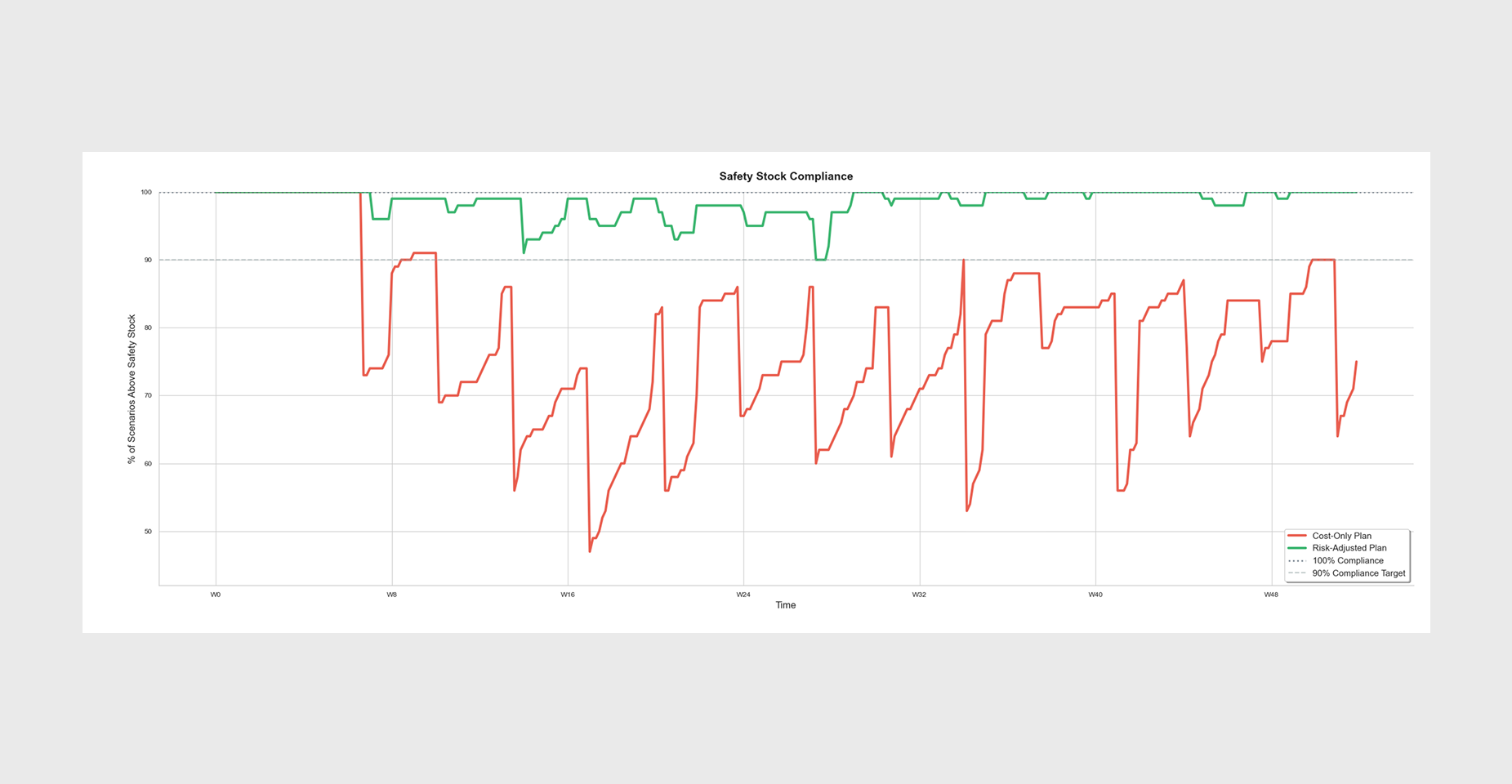
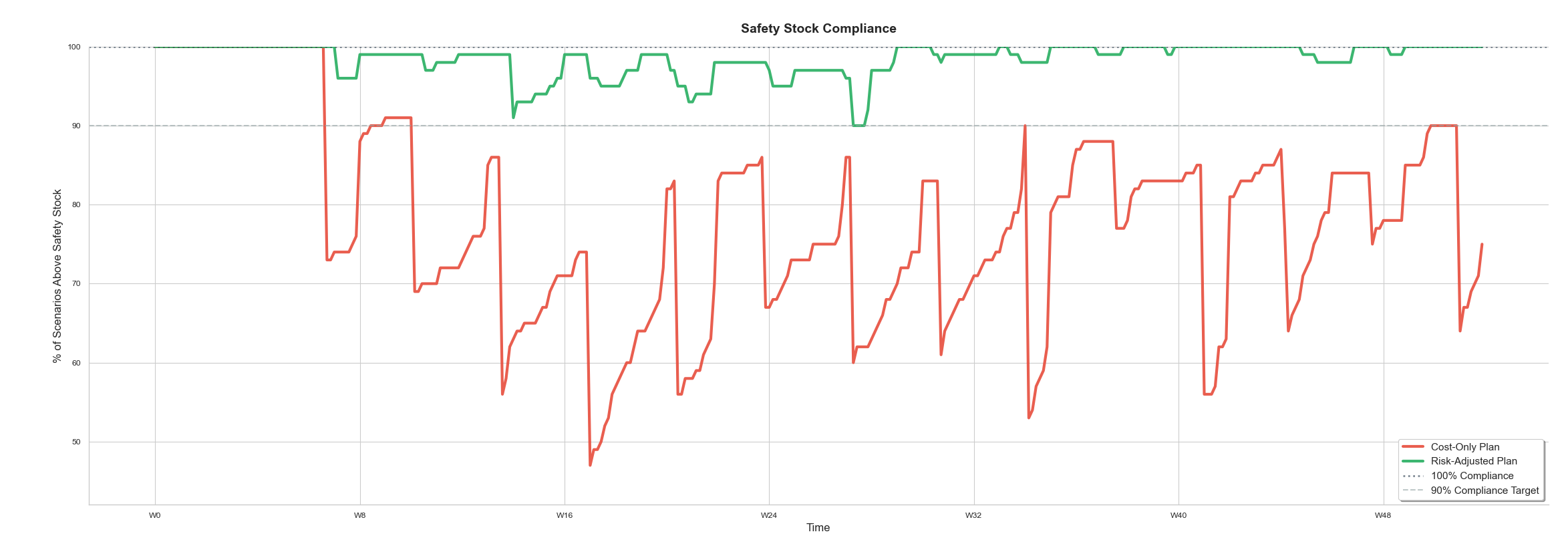
Putting this all together, we can run our optimizer and retrieve different plans based on our risk tolerance parameter, λ.

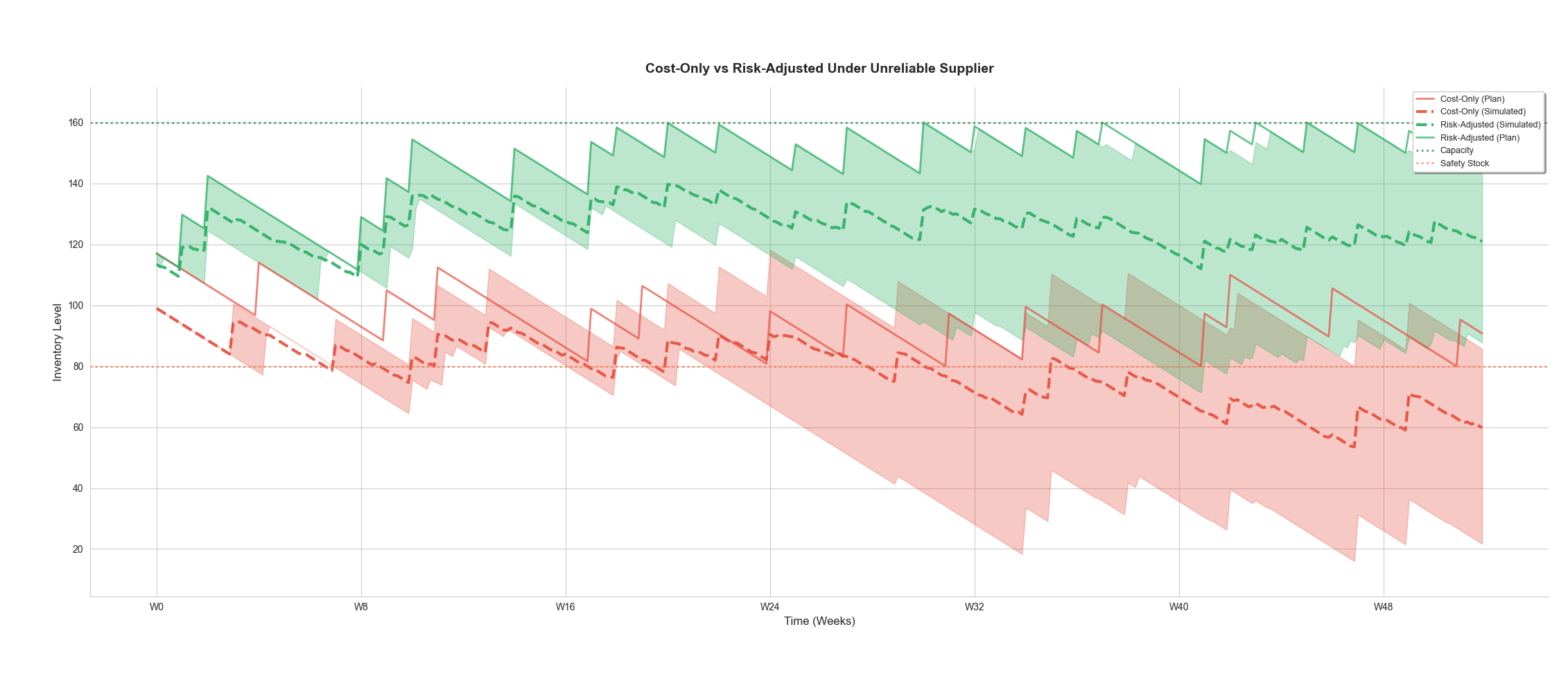
The green plot shows a plan that balances risk and cost, while the red plot optimizes solely for cost.

We run identical simulated scenarios against each plan, plotting the mean inventory level as a dashed line. The shaded areas represent the 20th to 80th percentile outcomes.

The cost-focused delivery plan clearly has a much higher probability of inventory shortages due to potential delays. Note how frequently the red scenarios dip below the orange "safety stock" level.

Ultimately, the risk-adjusted methodology leads to ~20% improvement in simulated safety stock compliance rate.

‍

Production Lessons and Practitioner Insights

Implementation Strategy: "Hard First, Soften Later"

Phase 0: Evaluate & quantify risk metrics using scenario modeling

Phase 1: Start with hard diversity constraints to establish baseline risk mitigationPhase 2: Transition to soft penalties once comfortable with stochastic framework

Phase 3 (optional): Increase scenario modeling sophistication and multi-objective optimization

‍

When to Use Each Approach

• Deterministic optimization: Stable supply chains with predictable suppliers
• Hard constraints: Regulatory requirements or risk-averse organizations
• Stochastic optimization: Dynamic environments with quantifiable disruption patterns

‍

Why Stochastic Supply Chain Optimization Matters

Traditional supply chain optimization treats uncertainty as an afterthought, resulting in brittle schedules that fail under realistic disruptions. Our stochastic programming approach recognizes that supply chain management is fundamentally about decision-making under uncertainty.

The result is a supply chain optimization framework that balances cost efficiency with operational resilience, delivering measurable profit improvements while reducing the risks of catastrophic failure.

‍